Interpolace a komprese obrazových dat

Dnes se dozvíte, co je interpolace a komprese digitálních obrazových souborů. Není to jako v klasické fotografii. Špičkové čidlo a optika není zdaleka jedinou podmínkou kvalitní digitální fotografie. Interpolace nasnímaných dat může výrazně zlepšit nebo naopak zhoršit výsledný fotografický obraz. Komprese datových souborů nasnímaných fotoaparátem nebo skenerem vám může ušetřit hodně peněz za drahé paměťové karty.
V minulé fotoškole jste se dozvěděli o tom, jak se světlocitlivým čidlem snímá barevný obraz. V současné době je zdaleka nejčastěji používanou technologií světlocitlivé čidlo překryté barevným mozaikovým filtrem. Čidlo se 4 milióny světlocitlivých elementárních buněk pokryté mozaikovým filtrem typu GRGB pak nasnímá 2 milióny zelených (G) pixelů, jeden milión červených ® a jeden milión modrých (B). Abychom získali kompletní informaci o barvě v určitém místě, potřebujeme zkombinovat buňky všech tří základních barev. Minimální velikost elementární buňky CCD čidla se dnes pohybuje kolem 5 mikronů. Protože rozlišovací schopnost oka je řádově menší, existuje zde prostor pro matematické dopočítání pixelů. Tento postup se nazývá matematická interpolace. Dostatečné množství přesně definovaných barevných pixelů je základním předpokladem pro kvalitní zobrazení a tisk.
Co je matematická interpolace?
Interpolace je matematická technika, kterou je stávající rastr obrazových bodů sejmutých v relativně nízkém rozlišení, doplňován v mezilehlých sloupcích a linkách. Odstín nově dopočítaných bodů vždy leží mezi dvěma sousedními čidlem změřenými body. Při použití vhodného algoritmu tak lze ve srovnání s původním, čidlem změřeným obrazem, dosáhnout měkčích (postupných) barevných přechodů a tím i celkově lepšího vzhledu.
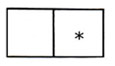
Schémata nejběžnějších matematických interpolací jsou ukázána na obr.1
 |
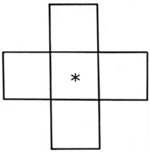 |

Na obrázcích je ukázáno, z jakých pixelů (prázdné čtverečky obr.1) se dopočítává pixel označený hvězdičkou. Interpolace na obr.1 dopočítává jen podle sousedního elementu v řádce nebo sloupci. Z hlediska výpočtu je nejnáročnější schema interpolace na obr.3, kde se dopočítává z největšího počtu elementů. Způsoby, kterými fotoaparát dopočítává pixely, patří k nejvíce střeženým firemním tajemstvím. Tyto výpočty totiž výrazně ovlivňují kvalitu obrazu. Nejobtížnější jsou samozřejmě interpolace v místech ostrých kontrastů světla, podle kterých hodnotíme ostrost kresby. Lze předpokládat, že počítač může v rámci jednoho snímku používat několik způsobů interpolace. Efektivitě matematické interpolace napomáhá i tvar a geometrické rozmístění světlocitlivých elementů. Elementy s hexagonálním tvarem, které ve svých čidlech používá např. firma Fuji, jsou vzhledem k menším vzdálenostem mezi elementy výhodnější pro interpolace. Interpolované pixely však nemohou nahradit pixely fyzikálně změřené. Interpolací nelze zvýšit množství primárně získané informace. Jedná se jen o postup, kterým lze tuto primárně získanou informaci lépe využít ke kvalitnějšímu zobrazení. Foveon umí zachytit 4 milióny pixelů s plnou informací o barvě. Neuděláme s ním však čtyřikrát větší zvětšeninu o stejné kvalitě ve srovnání se 4 megapixelovým čidlem s filtrovou mozaikou. To by platilo, pokud by se nepoužila interpolace.
- Předchozí strana
- 1
- 2
- 3
- Další strana




















Komentáře
Zobrazit diskusi ke článku ve fóruLineární interpolace se jmenuje lineární, protože se interpolovaná hodnota stanoví tak, že se známými hodnotami v sousedních bodech proloží přímka. K tomu jsou ovšem zapotřebí dva sousední body, nikoliv jen jeden. To, co je v článku chybně označeno jako lineární interpolace, není lineární interpolace, ale o řád nižší interpolace nejbližším sousedem. Naznačené schéma kvadratické interpolace vypadá také dost záhadně - tam těch sousedních bodů, které jsou zapotřebí, pro změnu zase přebývá. Kromě toho, kvadratická interpolace není zrovna příliš běžná. Mnohem častěji než kvadratická interpolace, se používá interpolace kubická nebo bikubická. Srovnávací studie různých druhů interpolace používaných u CCD elementů s klasickým CFA chipem je k nalezaní zde: http://ise0.stanford.edu/~tingchen/.
Přiznám se, že se nepovažuji za odborníka na matematické operace při interpolacích dat. U lineární interpolace je jasné, že přímka je definována dvěma body. Proto tím jedním bodem myslím bod sousední. V článku jde v tomto případě o vysvětlení koncepce. Se zvyšujícím se počtem bodů uvažovaným ve výpočtů roste kvalita interpolace, na druhé straně se zvyšuje nárok na výkon výpočetního procesoru a zároveň se prodlužuje i doba výpočtu.
"U lineární interpolace je jasné, že přímka je definována dvěma body. Proto tím jedním bodem myslím bod sousední." Promiňte, ale lineární interpolace je velmni rozšířený, zavedený pojem a nemůžete dle libosti volně používat pro úplně jiný typ interpolace (který je navíc běžně známý pod jiným jménem). To, co jste zde právě napsal, je nesmysl. V bodě, kde interpolujete, hodnotu neznáte. Tu teprve chcete najít, Tudíž tou hodnotou nemůžete nic prokládat. Určíte ji až později, na základě funkce proložené známými hodnotami. U lineární interpolace prokládáte ***známými*** hodnotami přímku a proto potřebujete vždy dva sousení body, kde tu hodnotu znáte. Stejně tak u kvadratické interpolace prokládáte kvadratickou funkci a kvadratická funkce je určená mnohem menším počtem bodů, než jaký naznačuje vaše schéma v článku.
Máte pravdu s tím názvem kvadratické interpolace. Je jasné, že polÿnom druhého stupně (kvadratická interpolace) s třemi koeficienty nestačí na tenhle počet bodů. Názvy ze schématu odstraním. Byly převzaty z fotografické literatury, která nebyla psána matematikem a v okmžiku, kdy mě na to upozorňujete, vidím, že to matematicky nehraje. Článek není o tom, jak se přesně výpočty provádějí. Docela by mě to zajímalo čím se liší interpolace u Kodaku , Fuji ..... Pochybuji, že tohle tady v Čechách někdo ví. Díky za komentář a přesné vysvětlení..
Pro vkládání komentářů musíte být přihlášen.